¶关系代数运算符
集合运算符
| 运算符 | 含义 | 英文 |
|---|---|---|
| $∪$ | 并 | Union |
| $−$ | 差 | Difference |
| $∩$ | 交 | Intersection |
| $×$ | 笛卡尔积 | Cartesian Product |
比较运算符
| 运算符 | 含义 |
|---|---|
| $>$ | 大于 |
| $≥$ | 大于等于 |
| $<$ | 小于 |
| $≤$ | 小于等于 |
| $=$ | 等于 |
| $≠$ | 不等于 |
专门的关系运算符
| 运算符 | 含义 | 英文 |
|---|---|---|
| $σ$ | 选择 | Selection |
| $π$ | 投影 | Projection |
| $⋈$ | 链接 | Join |
| $÷$ | 除 | Division |
逻辑运算符
| 运算符 | 含义 |
|---|---|
| $∧$ | 与 |
| $∨$ | 或 |
| $¬$ | 非 |
¶5 种基本的关系代数运算
¶并(Union)
关系 R 与 S 具有相同的关系模式,即 R 与 S 的元数相同(结构相同),R 与 S 的并是属于 R 或 属于 S 的元组构成的集合,记作 R ∪ S,定义如下:
¶差(Difference)
关系 R 与 S 具有相同的关系模式,关系 R 与 S 的差是属于 R 且 不属于 S 的元组构成的集合,记作 R − S,定义如下:
¶广义笛卡尔积(Extended Cartesian Product)
两个无数分别为 n 目和 m 目的关系 R 和 S 的 笛卡尔积是一个 (n+m) 列的元组的集合。组的前 n 列是关系 R 的一个元组,后 m 列是关系 S 的一个元组,记作 R × S,定义如下:
$(t^n,t^m)$ 表示元素 $t^n$ 和 $t^m$ 拼接成的一个元组
¶投影(Projection)
投影运算是从关系的垂直方向进行运算,在关系 R 中选出若干属性列 A 组成新的关系,记作 $π_A(R)$,其形式如下:
¶选择(Selection)
选择运算是从关系的水平方向进行运算,是从关系 R 中选择满足给定条件的元组,记作 $σ_F(R)$,其形式如下:
¶实例
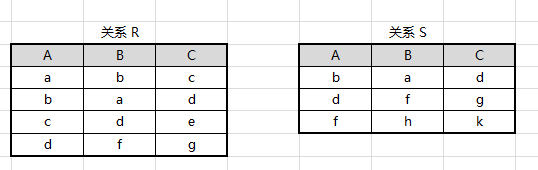
设有关系 R、S 如图所示,求 $R∪S$、 $R−S$、 $R×S$、 $π_{A,C}(R)$、 $σ_{A>B}(R)$ 和 $σ_{3<4}(R×S)$
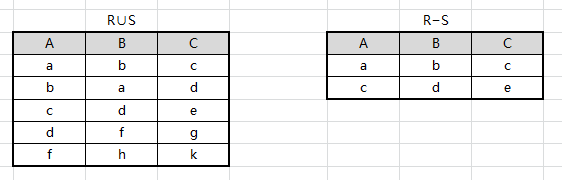
进行并、差运算后结果如下:
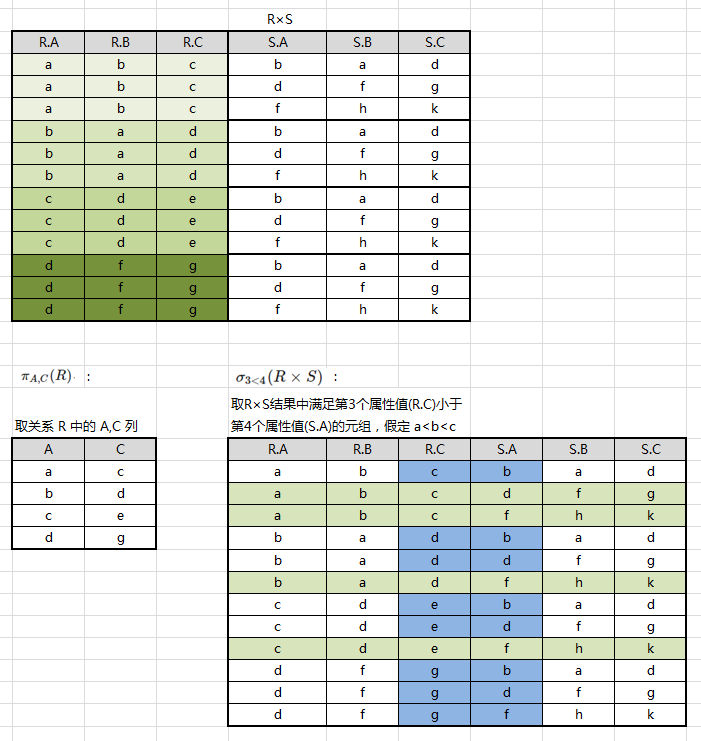
进行笛卡尔、 投影、 选择运算后结果如下:
¶扩展的关系代数运算
¶交(Intersection)
关系 R 和 S 具有相同的关系模式,交是由属于 R 同时双属于 S 的元组构成的集合,记作 R∩S,形式如下:
¶链接(Join)
注:下面的 θ 链接应该记作: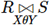
¶θ 链接
从 R 与 S的笛卡尔积中选取属性间满足一定条件的元组,可由基本的关系运算笛卡尔积和选取运算导出,表示为:
XθY 为链接的条件,θ 是比较运算符,X 和 Y 分别为 R 和 S 上度数相等且可比的属性组
例如:求 $R \Join_{R.A<S.B} S$,如果为:
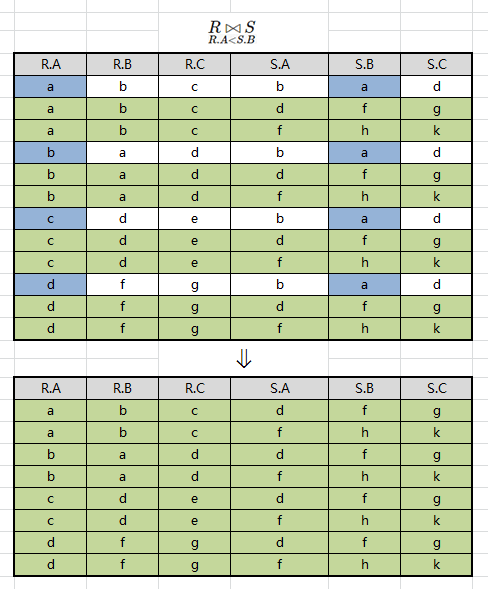
¶等值链接
当 θ 为「=」时,称之为等值链接,记为: $R\Join_{X=Y}S$
¶自然链接
自然链接是一种特殊的等值链接,它要求两个关系中进行比较的分量必须是 相同的属性组,并且在结果集中将 重复的属性列 去掉
例如:设有关系 R、S 如图所示,求 $R \Join S$
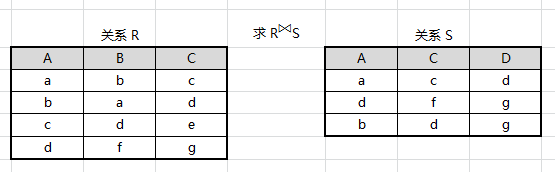
先求出笛卡尔积 $R×S$,找出比较分量(有相同属性组),即: R.A/S.A 与 R.C/S.C
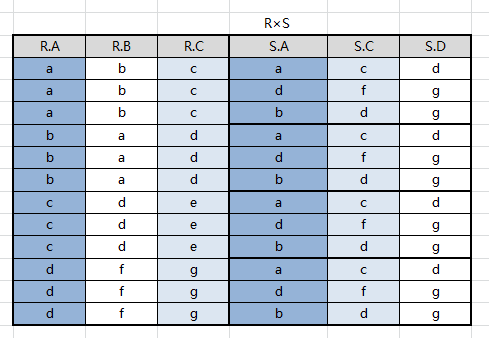
取等值链接 $R.A = S.A$ 且 $R.C = S.C$
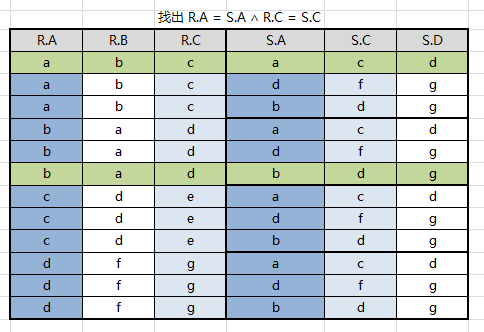
结果集中去掉重复属性列,注意无论去掉 R.A 或者 S.A 效果都一样,因为他们的值相等,结果集中只会有属性 A、B、C、D
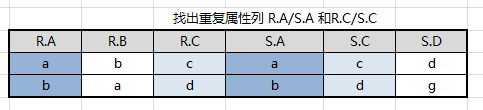
最终得出结果
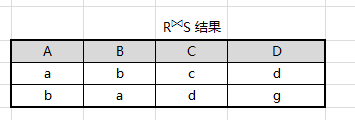
¶除(Division)
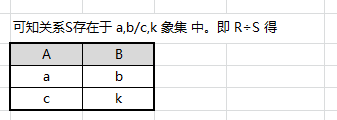
设有以下如图关系,求 $R÷S$
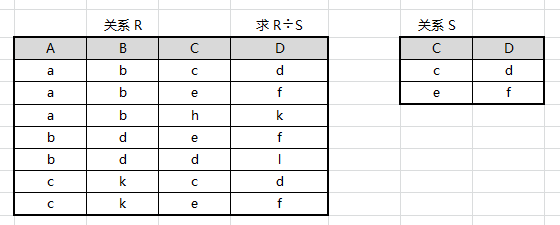
取关系 R 中有的但 S 中没有的属性组,即:A、B
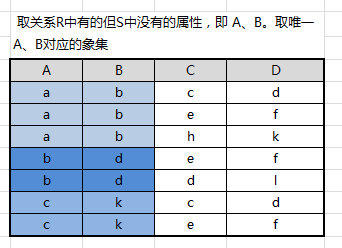
取唯一 A、B 属性组值的象集
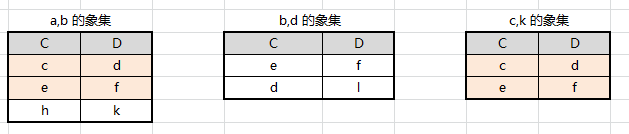
可知关系S存在于 a,b/c,k 象集 中。即 $R÷S$ 得